Is double AES more secure? The answer is YES, but it is not much more secure as you expect.
Do you remember why to use 3DES instead of double DES? The reason is double DES can be compromised with meet-in-the-middle-attack.
Time taken for DES with a 56 bits key size is 2^56. How about double DES with different keys? The time take is not expected to 2^112. It is smaller than 2^63 by using meet-in-the middle-attack, that is developed by Merkle and Hellman.
The result can be applied to any block ciphers including AES. For example, time taken for AES with a 128 bits key size is 2^128. Time taken with double AES with different keys is much smaller than 2^256. It is,
Time = 2^128 x log (2^128) + 2^128 x log (2^128) << 2^256
-Count
A blog of computer science that covers cryptography, UEFI BIOS, programming language, software applications, and network communication.
Monday, December 26, 2016
Saturday, December 24, 2016
Why is 2-round Feistel not Secure PRP?
The theorem, Luby-Rackoff'85, describes that, 3-round Feistel is a secure PRP if f is a secure PRF. I have many questions,
- Why 3-round?
- Is 2-round a secure PRP?
- Is 1-round a secure PRP?
Now, we use the below picture to check if 1-round Feistel a secure PRP?
We specify
Funcs [M, C] as set of all functions from M to C.
We specify
F as the 1-round Feistel.
F: K x M ---> C,
where
K is a key space,
M = {0,1}^(2n), is a message space,
C = {0,1}^(2n), is a cipher text space.
f1 is a secure PRP
f1: K x {0,1}^n ---> {0,1}^n
After we input a message
m = R || L,
,the output cipher text is
c = L1 || R.
When we check the cipher text and the message, we can say that the cipher text is produced by F because the left block of the cipher text is R that comes from the right block of the message. Therefore F is distinguishable from the Funcs. F is not sure PRP.
OK, Let's use the below picture to check if 2-round Feistel is secure PRP.
We specify
F as the 2-round Feistel.
F: K x M ---> C,
where
K is a key space,
M = {0,1}^(2n), is a message space,
C = {0,1}^(2n), is a cipher text space.
f1 and f2 are secure PRP
the output cipher text are ca, cb.
ma = R || La ---> ca = R2a1 || La1
mb = R || Lb ---> cb = R2b1 || Lb1
We observe that.
La1 = La xor f1(R)
Lb1 = Lb xor f1(R)
La1 xor Lb1 = La xor Lb ---- (formula 1)
When we check the two cipher texts and the two messages with this formula 1, we can say that they are produced by F. Therefore F is distinguishable from the Funcs. F is not sure PRP.
-GY
Wednesday, November 2, 2016
CMAC and CCM
We are confused about CMAC and CCM. Especially what does mean AES-CMAC or AES-CCM? They are defined in the following specfications.

Terminology
MAC is a short piece of information used to authetnicate a message. There are two types of MAC, hash function based MAC and cipher based MAC.
The implementations of hash function based MAC, abbreviated HMAC, are HMAC-MD5, HMAC-SHA1, and HMAC-SHA256. The postfix (e.g -MDB, -SHA1, or -SHA256) is the hash function used in the MAC.
CBC-MAC is a cipher based MAC. CMAC is variation of CBC-MAC that has security deficiencies. AES-CMAC and TDEA CMAC are implementation of CMAC.
ECB, CBC, and CCM are block cipher modes. CCM is an adaption of CBC and is counter with CBC-MAC. AES-CCM is only one implementation of CCM.
In conclusion,
-Count
- NIST 800-38B CMAC
- NIST 800-38C CCM
- RFC 4493 AES-CMAC
- RFC 3610 Counter with CBC-MAC (CCM)
After I read them. I made conclusion that:
- CMAC is used for authentication.
- CCM is used for authentication and confidentiality.
- CBC-MAC, CMAC, and CCM have some differences.
I draw the below picture to explain their relationships.

Terminology
- MAC - Message Authentication Code
- HMAC - Hash-Based MAC
- CBC-MAC - Cipher Block Chaining MAC
- CMAC - Cipher-Based MAC
- CBC - Cipher Block Chaining
- CCM - Counter with CBC-MAC
- ECB - Electronic Code Book
MAC is a short piece of information used to authetnicate a message. There are two types of MAC, hash function based MAC and cipher based MAC.
The implementations of hash function based MAC, abbreviated HMAC, are HMAC-MD5, HMAC-SHA1, and HMAC-SHA256. The postfix (e.g -MDB, -SHA1, or -SHA256) is the hash function used in the MAC.
CBC-MAC is a cipher based MAC. CMAC is variation of CBC-MAC that has security deficiencies. AES-CMAC and TDEA CMAC are implementation of CMAC.
ECB, CBC, and CCM are block cipher modes. CCM is an adaption of CBC and is counter with CBC-MAC. AES-CCM is only one implementation of CCM.
In conclusion,
- AES-CMAC is a MAC, implemented by AES algorithm for authentication.
- AES-CCM is an AES cipher with CCM mode for authenticatino and confidentiality.
-Count
Sunday, October 30, 2016
Use a computer to emulate devices of temperature connecting to AWS IoT
I modified the sample basicPubSub of the project aws-iot-device-sdk-python to develop the Python tool AwsIotPythonTest.py to test AWS IoT service.
My project is AwsIotPythonTest.
We can use the tool to emulate 3 connected devices, two sensors of temperature and one monitor. They are run in PC environment by opening 3 consoles. When running, they connect to AWS IoT service and exchange temperature information via MQTT as below picture.
My project is AwsIotPythonTest.
We can use the tool to emulate 3 connected devices, two sensors of temperature and one monitor. They are run in PC environment by opening 3 consoles. When running, they connect to AWS IoT service and exchange temperature information via MQTT as below picture.
The Sensor 1 and Sensor 2 devices connect to AWS IoT Service and publish temperature information to the service. The Monitor device connects to the service and subscribe it to receive temperature information coming from sensor devices. The publish/subscribe model follows MQTT. I described the idea of emulator in the project AwsIotPythonTest in details.
-Count
Thursday, October 27, 2016
How to use a computer as an IoT device to connect AWS IoT service?
Although we don't have Amazon IoT Button or other devices to try AWS IoT, please remember that our computers are devices. Therefore make them IoT.
The sample basicPubSub.py in AWS IoT Python SDK can help us do it.
We follow AWS IoT tutorial to create a device certificate. We download the device certificate, its root CA, and its private key in our local path where the sample exists.
We also create a policy, and a device. We attach both resources into the device certificate.
Because the command arguments of the sample are too long, I prefer to write a makefile Test.mk to test it.
E1 = a2uc??????????.iot.us-west-2.amazonaws.com
R1 = VeriSign-Class\ 3-Public-Primary-Certification-Authority-G5.pem
C1 = 5988??????-certificate.pem.crt
K1 = 5988??????-private.pem.key
dev1:
python3 basicPubSub.py -e $(E1) -r $(R1) -c $(C1) -k $(K1)
Run the sample.
>make -f Test.mk dev1
It will publish messages and receive subscribed messages in loop.

-Count
The sample basicPubSub.py in AWS IoT Python SDK can help us do it.
We follow AWS IoT tutorial to create a device certificate. We download the device certificate, its root CA, and its private key in our local path where the sample exists.
We also create a policy, and a device. We attach both resources into the device certificate.
Because the command arguments of the sample are too long, I prefer to write a makefile Test.mk to test it.
E1 = a2uc??????????.iot.us-west-2.amazonaws.com
R1 = VeriSign-Class\ 3-Public-Primary-Certification-Authority-G5.pem
C1 = 5988??????-certificate.pem.crt
K1 = 5988??????-private.pem.key
dev1:
python3 basicPubSub.py -e $(E1) -r $(R1) -c $(C1) -k $(K1)
Run the sample.
>make -f Test.mk dev1
It will publish messages and receive subscribed messages in loop.

-Count
Install AWS IoT Python SDK in Mac
I followed the steps in the page to install AWS IoT Python SDK in my MacBook but I occurred problem.
I checked my Python is version 3.
>python3 -V
Python 3.5.2
But the OpenSSL used by the Python is not 1.0.x that is required by the SDK.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 0.9.8zh 14 Jan 2016'
I used brew to download the new OpenSSL.
>brew update
>brew install openssl
>brew link —force openssl
The above command occurred warning.

The command cannot built a link in /usr/bin/openssl because the position is occupied by a real openssl file. I wanted to remove the below openssl but I couldn't.
>cd /usr/bin
>sudo rm -rf openssl
rm: openssl: Operation not permitted
I followed the page to remove it.
>csrutil disable
>reboot
>cd /usr/bin
>sudo rm -rf openssl
>csrutil enable
>reboot
At that time, I made sure that the old openssl was killed.
I built OpenSSL links.
>ln -s /usr/local/opt/openssl/lib/libcrypto.1.0.0.dylib /usr/local/lib/
>ln -s /usr/local/opt/openssl/lib/libssl.1.0.0.dylib /usr/local/lib/
>ln -s /usr/local/Cellar/openssl/1.0.2j/bin/openssl /usr/bin/openssl
I checked the Python's OpenSSL again, it was still 0.9.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 0.9.8zh 14 Jan 2016'
The python was installed in a PKG way and the OpenSSL 0.9.8 is embedded in the python. Therefore I wanted to remove the python.
I followed the page to uninstall the old Python 3.
1. Goto Finder>Applications>Python 3.0. Right click, select Move to Trash.
2.
>cd /Library/Frameworks/
>sudo rm -rf Python.framework
I used brew to install Python 3 with OpenSSL 1.0.2.
>brew install python3 --with-brewed-openssl
I checked the Python's OpenSSL again.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 1.0.2j 26 Sep 2016'
OKAY. I had upgrated Python and OpenSSL.
Then I downloaded the SDK and run a sample in my MacBook. The final steps followed the end of the page.
-Count
I checked my Python is version 3.
>python3 -V
Python 3.5.2
But the OpenSSL used by the Python is not 1.0.x that is required by the SDK.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 0.9.8zh 14 Jan 2016'
I used brew to download the new OpenSSL.
>brew update
>brew install openssl
>brew link —force openssl
The above command occurred warning.

The command cannot built a link in /usr/bin/openssl because the position is occupied by a real openssl file. I wanted to remove the below openssl but I couldn't.
>cd /usr/bin
>sudo rm -rf openssl
rm: openssl: Operation not permitted
I followed the page to remove it.
>csrutil disable
>reboot
>cd /usr/bin
>sudo rm -rf openssl
>csrutil enable
>reboot
At that time, I made sure that the old openssl was killed.
I built OpenSSL links.
>ln -s /usr/local/opt/openssl/lib/libcrypto.1.0.0.dylib /usr/local/lib/
>ln -s /usr/local/opt/openssl/lib/libssl.1.0.0.dylib /usr/local/lib/
>ln -s /usr/local/Cellar/openssl/1.0.2j/bin/openssl /usr/bin/openssl
I checked the Python's OpenSSL again, it was still 0.9.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 0.9.8zh 14 Jan 2016'
The python was installed in a PKG way and the OpenSSL 0.9.8 is embedded in the python. Therefore I wanted to remove the python.
I followed the page to uninstall the old Python 3.
1. Goto Finder>Applications>Python 3.0. Right click, select Move to Trash.
2.
>cd /Library/Frameworks/
>sudo rm -rf Python.framework
I used brew to install Python 3 with OpenSSL 1.0.2.
>brew install python3 --with-brewed-openssl
I checked the Python's OpenSSL again.
>python3
>>>import ssl
>>>ssl.OPENSSL_VERSION
'OpenSSL 1.0.2j 26 Sep 2016'
OKAY. I had upgrated Python and OpenSSL.
Then I downloaded the SDK and run a sample in my MacBook. The final steps followed the end of the page.
-Count
Install AWS IoT Python SDK in Windows
AWS IoT is an IoT platform provided by Amazon to connect devices in cloud. We can use the AWS IoT Python SDK to write Python script to access the AWS IoT platform through MQTT to interact with connected devices. The following are steps of installing the SDK.
Check if the current Python is version 3.
>python -V
Python 3.5.2 ...
I prefer to use Python 3. If it is not, we can download the newest Python 3.5.2 from the website and install it.
https://www.python.org/ftp/python/3.5.2/python-3.5.2.exe
Check the OpenSSL version used by the Python.
>>> import ssl
>>> ssl.OPENSSL_VERSION
'OpenSSL 1.0.2h 3 May 2016'
Install the AWS IoT Python SDK from source that contains samples.
>git clone https://github.com/aws/aws-iot-device-sdk-python.git
>cd aws-iot-device-sdk-python
>python setup.py install
Indeed, we can also install the SDK from pip, but it doesn't have samples.
>pip install AWSIoTPythonSDK
Run a sample
>cd samples/basicPubSub
>python basicPubSub.py
An error occurs.

This page has a workaround:
https://github.com/aws/aws-iot-device-sdk-python/issues/23
import os
import sys
import AWSIoTPythonSDK
sys.path.insert(0, os.path.dirname(AWSIoTPythonSDK.__file__))
# Now the import statement should work
from AWSIoTPythonSDK.MQTTLib import AWSIoTMQTTClient
Run the sample again.
>python basicPubSub.py -h

-Count
Check if the current Python is version 3.
>python -V
Python 3.5.2 ...
I prefer to use Python 3. If it is not, we can download the newest Python 3.5.2 from the website and install it.
https://www.python.org/ftp/python/3.5.2/python-3.5.2.exe
Check the OpenSSL version used by the Python.
>>> import ssl
>>> ssl.OPENSSL_VERSION
'OpenSSL 1.0.2h 3 May 2016'
Install the AWS IoT Python SDK from source that contains samples.
>git clone https://github.com/aws/aws-iot-device-sdk-python.git
>cd aws-iot-device-sdk-python
>python setup.py install
Indeed, we can also install the SDK from pip, but it doesn't have samples.
>pip install AWSIoTPythonSDK
Run a sample
>cd samples/basicPubSub
>python basicPubSub.py
An error occurs.

This page has a workaround:
https://github.com/aws/aws-iot-device-sdk-python/issues/23
import os
import sys
import AWSIoTPythonSDK
sys.path.insert(0, os.path.dirname(AWSIoTPythonSDK.__file__))
# Now the import statement should work
from AWSIoTPythonSDK.MQTTLib import AWSIoTMQTTClient
Run the sample again.
>python basicPubSub.py -h

-Count
Monday, October 24, 2016
Why cannot S-box of DES cipher be linear?
We cannot specify any S-box in DES cipher. One of the rules to choice of S-box is that, it cannot be linear. How do we understand it? Below is my explanation, but I'm not sure it is correct.
The Stanford on-line course, Cryptography I, describes that, if S-box is chosen as linear, the DES cipher would be linear.
DES(k, m) = B x |m |= c (statement 1)
|k1 |
|k2 |
|. |
|. |
|. |
|k16|
where:
|m| = |c| = 64 (bits)
|ki| = 48 (bits)
B is a 64x832 matrix.
The course describes that, "You just need 832 input output pairs, and you'll be able recover the entire secret key." How to explain the description? We can use a simple example:
Lets
B is 2 x 4 matrix.
|m| = |c| = |k| = 2 (bits)
We transform the statement 1 as below.
|b1 b2 b3 b4| x |m1| = |c1|
|b5 b6 b7 b8| |m2| |c2|
|k1|
|k2|
We give the below statement.
b1m1 xor b2m2 xor b3k1 xor b4k2 = c1 (statement 2)
b5m1 xor b6m2 xor b7k1 xor b8k2 = c2 (statement 3)
We assume that, we don't know any b and any k, but we know the input m and output c.
For statement 2, the number of unknown variables is 4. They are,
b1, b2, b3k1, b4k2.
For statement 3, the number of unknown variables is 4. They are,
b5, b6, b7k1, b8k2.
Total number of unknown variables is 8. Therefore we need 8 equations to derive all values of b and k.
Because,
|m| = |c| = 2
Each input/output pair has 2 equations. That is why we need 8/2 = 4 pairs of input/output to derive all values of b and k.
-Count
The Stanford on-line course, Cryptography I, describes that, if S-box is chosen as linear, the DES cipher would be linear.
DES(k, m) = B x |m |= c (statement 1)
|k1 |
|k2 |
|. |
|. |
|. |
|k16|
where:
|m| = |c| = 64 (bits)
|ki| = 48 (bits)
B is a 64x832 matrix.
The course describes that, "You just need 832 input output pairs, and you'll be able recover the entire secret key." How to explain the description? We can use a simple example:
Lets
B is 2 x 4 matrix.
|m| = |c| = |k| = 2 (bits)
We transform the statement 1 as below.
|b1 b2 b3 b4| x |m1| = |c1|
|b5 b6 b7 b8| |m2| |c2|
|k1|
|k2|
We give the below statement.
b1m1 xor b2m2 xor b3k1 xor b4k2 = c1 (statement 2)
b5m1 xor b6m2 xor b7k1 xor b8k2 = c2 (statement 3)
We assume that, we don't know any b and any k, but we know the input m and output c.
For statement 2, the number of unknown variables is 4. They are,
b1, b2, b3k1, b4k2.
For statement 3, the number of unknown variables is 4. They are,
b5, b6, b7k1, b8k2.
Total number of unknown variables is 8. Therefore we need 8 equations to derive all values of b and k.
Because,
|m| = |c| = 2
Each input/output pair has 2 equations. That is why we need 8/2 = 4 pairs of input/output to derive all values of b and k.
-Count
Sunday, October 23, 2016
Use BinToImg.py to analyze UEFI BIOS
We can use BinToImg.py to analyze UEFI BIOS. Below is the input files.
We use the below commands to generate PNG files with black-white bit pixels from the input files.
python3 BinToImg.py -w 6000 BIOS.rom
python3 BinToImg.py -w 6000 SPI0.bin
The option -w 6000 means that the tool generates an image of which width is 6000 pixels.
Below are the generated PNG files. I consider any BIOS engineer know what happens by observing these images, especially for BIOS.rom.png and SPI1.bin.png.
BIOS.rom.png

SPI1.bin.png

SPI0.bin.png

-Count
- BIOS.rom - A capsule file built by EDK build system.
- SPI0.bin - A binary file dumped from SPI ROM 0 after first booting.
- SPI1.bin - A binary file dumped from SPI ROM 1 after first booting.
The tool BinToImg.py transfers a byte to 8 pixels with black-white color. For example,
Byte = 55h = 01010101
Pixels
= 1 -> 0 -> 1 -> 0 -> 1 -> 0 ->1 -> 0
= 1 -> 0 -> 1 -> 0 -> 1 -> 0 ->1 -> 0
= black, white, black, white, black, white, black, white
We use the below commands to generate PNG files with black-white bit pixels from the input files.
python3 BinToImg.py -w 6000 BIOS.rom
python3 BinToImg.py -w 6000 SPI0.bin
python3 BinToImg.py -w 6000 SPI1.bin
The option -w 6000 means that the tool generates an image of which width is 6000 pixels.
Below are the generated PNG files. I consider any BIOS engineer know what happens by observing these images, especially for BIOS.rom.png and SPI1.bin.png.
BIOS.rom.png

SPI1.bin.png

SPI0.bin.png

-Count
Friday, October 21, 2016
Cross Platform Random Bitmap Generator
I created a project, RandomBitmap, in the below GitHub.
https://github.com/CountChu/RandomBitmap
There are two purposes of the project:
https://github.com/CountChu/RandomBitmap
There are two purposes of the project:
- to check if random variables generated by a specified platform (e.g., Windows, Android) are secure.
- to check if a file is random or has patterns by observing the black-white bitmap file transformed by the file.
This idea comes from the page, Pseudo-Random vs. True Random. The author uses PHP to transform random numbers to a bitmap. I separated the transformation into two Python programs, GenRandom.py and BinToImg.py because I want to test random number generators on different platforms as the below picture.
GenRandom, is a set of tools written by different languages on different platforms, calls a specified random generator to produce random numbers. These numbers will be saved in a file. The different languages are specified from the below reasons:
- Python is a cross platform language so that I can use GenRandom.py to test Windows, Linux, and MAC.
- For Android device, Java is a candidate language. Therefore I'll create a Java version tool, GenRandom.java, to test Android's random generator.
- For security IC or UEFI environment, C is a candidate language. The C version tool is named GenRandom.c.
- For Chrome Browser's Native Client written by C/C++, the tool will be named GenRandom.c. I'll use it to test random generators of OpenSSL and LIBC in Native Client environment.
- C# is the first candidate language in, I'll have a C# version, GenRandom.cs, to test Windows CNG.
RandomGenerator.py provides different random generators that are consumed by GenRandom.py:
- rg1() is a Python default random generator that is random.randint().
- rg2() is a random generator comes from the page.
BinToImg.py is a python tool that transforms data in a file into an PNG image file with black-white pixels so that we can observe the image to check if these numbers are random. The tool can be used independently. For example, we input any type of file in the tool to generate an picture with black-white pixels to check if the file is randomly.
I use the both tools to verify if the MAC random generator is secure.
>python GenRandom.py Random.bin
>python BinToImg.py Random.bin
I use the tool BinToImg.py to check a PDF file. We can find some patterns in the below picture.
>python BinToImg.py One.pdf
-Count
Saturday, October 15, 2016
If PRG is secure, PRG is unpredictable
Below is the definition of secure PRG.


Below is the definition of predictable PRG.

How do we proof the below theorem?
PRG is secure => PRG is unpredictable
The previous page proofed it by:
PRG is predictable => PRG is not secure
This pare proofs it in a direct way. Before proofing it, I draw the below picture, where G is PRG, to understand the definition of secure PRG and unpredictable PRG.

We keep the picture in our mind and use simple formulas to proof it.
The fact is that G is secure:
Adv = |Pr [A (G) = 1] - Pr [A (r) = 1]| <= e (e is epsilon)
Because the statement, that is proofed by the page, is also true.
Pr [A (r) = 1] = 1/2
Therefore
Pr [A (G) = 1] <= 1/2 + e
We can transfer the statement from A to B for the definition of A that is a statistical test.
Pr [B (G|1...i+1) = G|i+1] <= 1/2 + e
Therefore G is unpredictable.
-Count

Below is the definition of predictable PRG.

How do we proof the below theorem?
PRG is secure => PRG is unpredictable
The previous page proofed it by:
PRG is predictable => PRG is not secure
This pare proofs it in a direct way. Before proofing it, I draw the below picture, where G is PRG, to understand the definition of secure PRG and unpredictable PRG.

We keep the picture in our mind and use simple formulas to proof it.
The fact is that G is secure:
Adv = |Pr [A (G) = 1] - Pr [A (r) = 1]| <= e (e is epsilon)
Because the statement, that is proofed by the page, is also true.
Pr [A (r) = 1] = 1/2
Therefore
Pr [A (G) = 1] <= 1/2 + e
We can transfer the statement from A to B for the definition of A that is a statistical test.
Pr [B (G|1...i+1) = G|i+1] <= 1/2 + e
Therefore G is unpredictable.
-Count
Use Advantage to Define Secure PRG
Below is the Advantage definition:


We use Advantage to define Secure PRG as below:

How do we understand the definition of secure PRG with Advantage? We can draw the below picture to describe the definition.

-Count
We use Advantage to define Secure PRG as below:

How do we understand the definition of secure PRG with Advantage? We can draw the below picture to describe the definition.

-Count
Understand that, One Time Pad (OTP) has perfect secrecy
A cipher (E, D) over (K, M, C) that is OTP if
K = M = C = {0, 1}^n
c = E(k, m) = k xor m
m = D(k, c) = k xor c
where c in C, k in K, m in M
OTP has perfect secrecy because |k| = |m|.
How do we understand the statement?
We can give a simple example.
K = M = C = {0, 1}^2
Below is the table of the OTP cipher.

We focus on c = 11 to guess the probability of m where k is a uniform random variable.
Pr[E(k, 00) = 11] = 1/4
Pr[E(k, 01) = 11] = 1/4
Pr[E(k, 10) = 11] = 1/4
Pr[E(k, 11) = 11] = 1/4
It describes that the OTP is perfect secrecy because
Pr[E(k, m) = c] = 1/4, for all c in C,
where k is a uniform random variable.
-Count
K = M = C = {0, 1}^n
c = E(k, m) = k xor m
m = D(k, c) = k xor c
where c in C, k in K, m in M
OTP has perfect secrecy because |k| = |m|.
How do we understand the statement?
We can give a simple example.
K = M = C = {0, 1}^2
Below is the table of the OTP cipher.

We focus on c = 11 to guess the probability of m where k is a uniform random variable.
Pr[E(k, 00) = 11] = 1/4
Pr[E(k, 01) = 11] = 1/4
Pr[E(k, 10) = 11] = 1/4
Pr[E(k, 11) = 11] = 1/4
It describes that the OTP is perfect secrecy because
Pr[E(k, m) = c] = 1/4, for all c in C,
where k is a uniform random variable.
-Count
Tuesday, October 11, 2016
Perfect Secrecy ==> Key Length >= Message Length
Here is a theorem:
If a cipher (E, D) over (K, M, C) is a perfect secrecy,
then k length >= m length, where k is K, and m is M.
How do we proof it?
We transfer the theorem as below.
If k length < m length, the cipher is not a perfect secrecy.
Therefore we just give an example to explain the theorem.
Lets
K = {0, 1}^2 = {00, 01, 10, 11}
M = {0, 1}^3 = {000, 001, ..., 111}
C = {0, 1}^3 = {000, 001, ..., 111}
Obviously k length = 2 and m length = 3
Give a table.
M K C
--- -- ---
000 00 000
001 01 001
010 10 010
011 11 011
100 100
101 101
110 110
111 111
I consider it may be easy to explain the theorem if specifying elements in the table as numeric symbols.
M K C
- - -
0 0 0
1 1 1
2 2 2
3 3 3
4 4
5 5
6 6
7 7
We understand the meaning of "Perfect Secrecy". We focus c=0 and try to guess the message.
We know that
E(k, m) = c
D(k, c) = m
We can design a cipher (E, D) for c=0 and for all k is k as below.
D = {(k,c,m)}
where
k c m
- - -
0 0 0
1 0 1
2 0 2
3 0 3
There is a problem that the number of keys is not enough to cover another m values:4, 5, 6, 7.
Because k is a uniform random number, we expand the probability as below.
Pr[E(k,0)=0] = 1/4
Pr[E(k,1)=0] = 1/4
If a cipher (E, D) over (K, M, C) is a perfect secrecy,
then k length >= m length, where k is K, and m is M.
How do we proof it?
We transfer the theorem as below.
If k length < m length, the cipher is not a perfect secrecy.
Therefore we just give an example to explain the theorem.
Lets
K = {0, 1}^2 = {00, 01, 10, 11}
M = {0, 1}^3 = {000, 001, ..., 111}
C = {0, 1}^3 = {000, 001, ..., 111}
Obviously k length = 2 and m length = 3
Give a table.
M K C
--- -- ---
000 00 000
001 01 001
010 10 010
011 11 011
100 100
101 101
110 110
111 111
I consider it may be easy to explain the theorem if specifying elements in the table as numeric symbols.
M K C
- - -
0 0 0
1 1 1
2 2 2
3 3 3
4 4
5 5
6 6
7 7
We understand the meaning of "Perfect Secrecy". We focus c=0 and try to guess the message.
We know that
E(k, m) = c
D(k, c) = m
We can design a cipher (E, D) for c=0 and for all k is k as below.
D = {(k,c,m)}
where
k c m
- - -
0 0 0
1 0 1
2 0 2
3 0 3
There is a problem that the number of keys is not enough to cover another m values:4, 5, 6, 7.
Because k is a uniform random number, we expand the probability as below.
Pr[E(k,0)=0] = 1/4
Pr[E(k,1)=0] = 1/4
Pr[E(k,2)=0] = 1/4
Pr[E(k,3)=0] = 1/4
Pr[E(k,4)=0] = 0
Pr[E(k,4)=0] = 0
Pr[E(k,5)=0] = 0
Pr[E(k,6)=0] = 0
Pr[E(k,7)=0] = 0
It describes that the cipher is not perfect secrecy because
Pr[E(k,m)=0] = 1/4 or 0, for all k is in K.
Let me explain it in English. If we know the ciphertext c is 0 and the cipher algorithm, (E, D), we can guess the message, m:
-Count
It describes that the cipher is not perfect secrecy because
Pr[E(k,m)=0] = 1/4 or 0, for all k is in K.
Let me explain it in English. If we know the ciphertext c is 0 and the cipher algorithm, (E, D), we can guess the message, m:
- The event, m=4, 5, 6, or 7, doesn't happen.
- The probability of the event, m=0, 1, 2, 3, is 1/4.
-Count
How does a software engineer understand "Perfect Secrecy"?
I consider, a definition in mathematic formula format is like source code written with a computer language. Mathematic formula is written for mathematician. Source code is written for a computer.
The way to understand a mathematic definition is the same as the way to understand a source code. How do we understand source code? I believe any experienced software engineers know the trick. I also believe we can understand some mathematic definition in the same way for understanding source code.
Don't worry, we have enough ability to understand some mathematic definition. For example, below is the definition of "perfect secrecy":
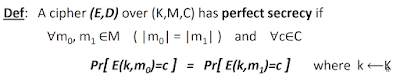
The definition is a formula that is compressed from many sentences. How do we understand it? A better way is try to decompress the formula to get original sentences and understand them.
We know that,
E(k, m) = c
D(k, c) = m
I explain the perfect secrecy that:
Our purpose is to translate the four sentences into a formal definition with a formula.
First, try to translate the above sentences in a informal formula.
E(k?, m?) = c
It means:
Translate it into another informal formula.
E(k, m?) = c
where k is a uniform random variable on K
Because m is deterministic by D(k, c) = m, we translate it again.
E(k, mi) = c
where k is a uniform random variable on K
The way to understand a mathematic definition is the same as the way to understand a source code. How do we understand source code? I believe any experienced software engineers know the trick. I also believe we can understand some mathematic definition in the same way for understanding source code.
Don't worry, we have enough ability to understand some mathematic definition. For example, below is the definition of "perfect secrecy":
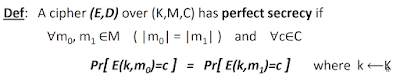
The definition is a formula that is compressed from many sentences. How do we understand it? A better way is try to decompress the formula to get original sentences and understand them.
We know that,
E(k, m) = c
D(k, c) = m
I explain the perfect secrecy that:
- I know the ciphertext, c.
- I know the encryption and decryption algorithms, E and D.
- It is hard to guess the key, k, because it is a uniform random variable. The probability of successfully guessing is 1/|K|.
- It is hard to get a correct m by decrypting c with a guessed key because the probability of getting the correct m is the same constant for all k in K.
Our purpose is to translate the four sentences into a formal definition with a formula.
First, try to translate the above sentences in a informal formula.
E(k?, m?) = c
It means:
- I know the ciphertext, c, and encryption algorithm, E.
- I don't know k and m.
Translate it into another informal formula.
E(k, m?) = c
where k is a uniform random variable on K
Because m is deterministic by D(k, c) = m, we translate it again.
E(k, mi) = c
where k is a uniform random variable on K
and i = 0, 1, ..., |M|
Finally we add the 4th sentence to complete the formal definition of "perfect secrecy".
Pr[E(k, mi) = c] = constant
where k is a uniform random variable on K
and i = 0, 1, ..., |M|
-Count
Negligible and non-negligible - A better explanation
The page, Negligible and non-negligible, explains what means
lambda >= lambda d
in the definition of negligible and non-negligible,

by using the below formula,
g(x) = 2^x - x^d >= 0
to draw the below picture,

Actually, we can using another formula to draw a more beautiful picture. We derive the formula as below:
We except that:
f(x) = 1/(2^x) <= 1/(x^d)
We define that:
g(x) = (x^d) / (2^x) <= 1
And draw the below picture for d = 2, 3, 4.

Please look at the red lines:
For d = 2, g(x) <= 1, if x >= 4
For d = 3, g(x) <= 1, if x >= 9.94...
For d = 4, g(x) <= 1, if x >= 16
The values, 4, 9.94..., and 16 are of "lambda d".
-Count
lambda >= lambda d
in the definition of negligible and non-negligible,

by using the below formula,
g(x) = 2^x - x^d >= 0
to draw the below picture,

Actually, we can using another formula to draw a more beautiful picture. We derive the formula as below:
We except that:
f(x) = 1/(2^x) <= 1/(x^d)
We define that:
g(x) = (x^d) / (2^x) <= 1
And draw the below picture for d = 2, 3, 4.

Please look at the red lines:
For d = 2, g(x) <= 1, if x >= 4
For d = 3, g(x) <= 1, if x >= 9.94...
For d = 4, g(x) <= 1, if x >= 16
The values, 4, 9.94..., and 16 are of "lambda d".
-Count
Monday, September 26, 2016
Uniform Random Variable v.s. Identify Function.
We know that a random variable r.v. is actually a function. Can we confirm that a uniform random variable must be an identity function? I don't think so. I also have not found that the identify function is a part of the definition of the uniform r.v. yet. Let me explain why.
Below is the r.v. definition:
X: U ---> V
Because r.v. is also a function, I like write it as below only for easily thinking for me.
f: X ---> Y
The uniform r.v. is defined as below.
f: X ---> Y, Y = X
Pr [f(x) = y] = 1 / |X|
Below is the definition of identity function.
f: X ---> X
f(x) = x for all x is X
We define two random variables, f1 and f2, with same X and Y as below.
X = {0, 1, 2, 3}
Y = {0, 1, 2, 3}
f1: X ---> Y
f2: X ---> Y
Obviously, f1 and f2 are uniform r.v. because
Below is the r.v. definition:
X: U ---> V
Because r.v. is also a function, I like write it as below only for easily thinking for me.
f: X ---> Y
The uniform r.v. is defined as below.
f: X ---> Y, Y = X
Pr [f(x) = y] = 1 / |X|
Below is the definition of identity function.
f: X ---> X
f(x) = x for all x is X
We define two random variables, f1 and f2, with same X and Y as below.
X = {0, 1, 2, 3}
Y = {0, 1, 2, 3}
f1: X ---> Y
f2: X ---> Y
Obviously, f1 and f2 are uniform r.v. because
Pr [f1(x) = y] = 1 / |X|
Pr [f2(x) = y] = 1 / |X|
but f2(x) is not an identity function because
Pr [f2(x) = y] = 1 / |X|
but f2(x) is not an identity function because
f2(x) <> x for all x is X.
However, we prefer to select the identity function, f1(x), as an uniform random variable.
So far, I answer the question myself because I have not found the answer on Internet yet.
So far, I answer the question myself because I have not found the answer on Internet yet.
-Count
Saturday, September 24, 2016
Summarize of Apple Watch unlocking Mac
The macOS Sierra was released on 9/20 this year. One of the most interesting feature, I think, is Apple Watch unlocking Mac. I tried the feature on 9/21, Chinese time. I'm summarizing it as below.
- Apple devices unlock model:
- Enable the unlocking feature in MacBook.
- Connect to Internet
- Setup Two-Factor Authentication via iCloud account (Apple ID).
- Specify the unlocked password for the MacBook that is different from iCloud account password.
- The unlock conditions:
- Apple Watch is unlocked.
- Direct Wi-Fi (It is not necessary to connect to Internet or to Wi-Fi station)and Bluetooth must be enabled.
- Apple Watch is near to MacBook.
- Press any key on MacBook or open the cover to unlock it.
-Count
How does a companion device verify the service HMAC comes from a Windows device?
The Windows Companion Device Framework (CDF) is a Windows framework that defines a security protocol between a Windows device and a companion device (e.g., Android phone.) so that a companion device can unlock a Windows device.
The question is, how does a companion device verify the service HMAC comes from a Windows device?
The answer was not provided by the old version of CDF site page, but I found, the answer appeared in the latest updated version, 9/19/2016.
In the Authentication protocol section, it describes:
Validate Service HMAC = HMAC (authentication key, service nonce||device nonce||session nonce).
I write the process of verification as below for coding better.
The question is, how does a companion device verify the service HMAC comes from a Windows device?
The answer was not provided by the old version of CDF site page, but I found, the answer appeared in the latest updated version, 9/19/2016.
In the Authentication protocol section, it describes:
Validate Service HMAC = HMAC (authentication key, service nonce||device nonce||session nonce).
I write the process of verification as below for coding better.
- The companion device accepts data from the Windows device.
- (HmacSrv, NonceSrv, NonceDk, NonceSk)
- It verifies the data by the formula.
- HmacSrv2 = HMAC-SHA256 (AuthKey, NonceSrv||NonceDk||NonceSk)
- It checks if HmacSrv equals to HmacSrv2.
- If yes, continue to unlock the Windows device.
Another question is why does the companion device need to verify HmacSrv? The reason is to make sure that data comes from the windows device that was trusted by the companion device because both has been registered each other in the registration process.
-Count
Tuesday, September 20, 2016
If PRG is predictable, PRG is insecure.
The Stanford on-line course, Cryptography I, proof that "If PRG is secure, PRG is unpredictable". The statement is equal to "If PRG is predictable, PRG is insecure".
Below is the definition of "predictable".

The steps of the proof are below.

(I'm sorry I directly copy the pictures from the course because it is hard to write the math statements by typing. If the original author concern it, please let me know and I'll remove them.)
The question is, why is the statement true?
Pr[B(r)=1] = 1/2
The statement in the probability
B(r)=1,
is equal to
A(r(i...i)) = r(i+1)
Let's calculate the probability.
A(r(i...i)) r(i+1)
----------- ------
0 0
0 1
1 0
1 1
We specify that
Pr[A=0] = p0
Pr[A=1] = p1
where p0 + p1 = 1
(We cannot say p0 = p1 = 1/2.)
Obviously,
Pr[r(i+1) = 0] = 1/2
Pr[r(i+1) = 1] = 1/2
because r is a uniform random variable.
Pr [A = r(i+1)] = Pr[A=0] * Pr[r(i+1)=0] + Pr[A=1] * Pr[r(i+1)=1]
= p0 * 1/2 + p1 * 1/2 = (p0 + p1) / 2 = 1/2.
because the i+1 bit is independent of the first i bits.
-Count
Below is the definition of "predictable".

The steps of the proof are below.

(I'm sorry I directly copy the pictures from the course because it is hard to write the math statements by typing. If the original author concern it, please let me know and I'll remove them.)
The question is, why is the statement true?
Pr[B(r)=1] = 1/2
The statement in the probability
B(r)=1,
is equal to
A(r(i...i)) = r(i+1)
Let's calculate the probability.
A(r(i...i)) r(i+1)
----------- ------
0 0
0 1
1 0
1 1
We specify that
Pr[A=0] = p0
Pr[A=1] = p1
where p0 + p1 = 1
(We cannot say p0 = p1 = 1/2.)
Obviously,
Pr[r(i+1) = 0] = 1/2
Pr[r(i+1) = 1] = 1/2
because r is a uniform random variable.
Pr [A = r(i+1)] = Pr[A=0] * Pr[r(i+1)=0] + Pr[A=1] * Pr[r(i+1)=1]
= p0 * 1/2 + p1 * 1/2 = (p0 + p1) / 2 = 1/2.
because the i+1 bit is independent of the first i bits.
-Count
What does mean "Advantage"
When I learn the Stanford online course, Cryptography I, I am confused on the Advantage definition:


The purpose is let Adv[A,G] be "negligible" . I can consider it is nearby zero. There are 4 cases of the Adv in the below table:
Pr[A(G(k))=1] Pr[A(r)=1] Adv[A,G]
------ ------------- ---------- --------
Case 1 0 0 0
Case 2 1 0 1
Case 3 0 1 1
Case 4 1 1 0
Be careful that:
The "0" in the table means nearby zero.
The "1" in the table means nearby one.
We don't care about case 1 and case 2 where,
Pr[A(r)=1] = 0.
The formula is equal to
Pr[A(r)=0] = 1,
that means the statistical test A determines the r is not random. Actually r is a uniform random variable on {0,1}^n. Therefore we cannot find any statistical test to determine r is not random.
For Case 3, the PRG, G, is bad because it is not random determined by the statistical test, A.
Therefore only Case 4 are what we concern. Why is the Adv "negligible" in Case 4? I consider the reason is,
Pr[A(G(k))=1]
is not exactly equals to one.
-Count


The purpose is let Adv[A,G] be "negligible" . I can consider it is nearby zero. There are 4 cases of the Adv in the below table:
Pr[A(G(k))=1] Pr[A(r)=1] Adv[A,G]
------ ------------- ---------- --------
Case 1 0 0 0
Case 2 1 0 1
Case 3 0 1 1
Case 4 1 1 0
Be careful that:
The "0" in the table means nearby zero.
The "1" in the table means nearby one.
We don't care about case 1 and case 2 where,
Pr[A(r)=1] = 0.
The formula is equal to
Pr[A(r)=0] = 1,
that means the statistical test A determines the r is not random. Actually r is a uniform random variable on {0,1}^n. Therefore we cannot find any statistical test to determine r is not random.
For Case 3, the PRG, G, is bad because it is not random determined by the statistical test, A.
Therefore only Case 4 are what we concern. Why is the Adv "negligible" in Case 4? I consider the reason is,
Pr[A(G(k))=1]
is not exactly equals to one.
-Count
Friday, September 16, 2016
Why has Apple removed PPTP VPN from iOS 10 and macOS Sierra 10.12?
When I upgraded my iPad and iPhone to iOS 10, my MacBook to macOS, I found that PPTP VPN was removed? Why did Apple decide to do it? I think the reason is, PPTP VPN is not secure. Why? The Stanford on-line course, Cryptography I, answers the question.
PPTP VPN uses the same key for encryption in both directions between client and server.
In the client side, the messages, m1, m2 and m3, are encrypted by G(k) before sending to the server. G is PRG.
CiphertextClient = [m1 || m2 || m3] xor G(k)
In the server side, the message, s1, s2, and s3, are encrypted by G(k) before sending to the client.
CiphertextServer = [s1 || s2 || s3] xor G(k)
If the ciphertext of client and server are intercepted, a hacker can break the ciphertext without knowing G(k) because,
CiphertextClient xor CiphertextServer =
[m1 || m2 || m3] xor [s1 || s2 || s3]
Even though client and server use stream cipher, it is still not secure because client and server share the same G(k).
That is also why TLS uses different key for encryption in both client and server.
-Count
PPTP VPN uses the same key for encryption in both directions between client and server.
In the client side, the messages, m1, m2 and m3, are encrypted by G(k) before sending to the server. G is PRG.
CiphertextClient = [m1 || m2 || m3] xor G(k)
In the server side, the message, s1, s2, and s3, are encrypted by G(k) before sending to the client.
CiphertextServer = [s1 || s2 || s3] xor G(k)
If the ciphertext of client and server are intercepted, a hacker can break the ciphertext without knowing G(k) because,
CiphertextClient xor CiphertextServer =
[m1 || m2 || m3] xor [s1 || s2 || s3]
Even though client and server use stream cipher, it is still not secure because client and server share the same G(k).
That is also why TLS uses different key for encryption in both client and server.
-Count
Thursday, September 15, 2016
Negligible and non-negligible
The Stanford online course, Cryptography I, describes:

What does mean "lambda >= lambda d"?
Because the epsilon is a function, we can write the lambda as x and the epsilon as f(x) for easy understanding. We specify f(x) as below, that is an example,
f(x) = 1 / (2^x)
The f(x) is negligible because,
f(x) = 1 / (2^x) <= 1 / (x^d),
for all d and large enough x. (statement 1)
Why do we consider the statement 1 is true? I am not a mathematician. I prefer to use enough examples and tools to observe and understand problem. The tool, the iPad App Quick Graph+, is used to draw curves of the below functions.
f(x) = 1 / (2^x)
f(x) = 1 / x
f(x) = 1 / (x^2)
f(x) = 1 / (x^3)
f(x) = 1 / (x^4)

It is hard to verify the statement 1 with the picture because the curves are close to each other when x is large. Therefore we transfer the statement 1 as below.
g(x) = 2^x - x^d >= 0,
for all d and an enough large x. (statement 2)
We give examples, d = 1, 2, 3, 4. The below picture contains the curves.

If we zoom in the picture, we can find an interesting thing.
The statement 2 is true for an enough large x.

For d = 1, g(x) = 2^x - x >= 0,
if x >= x1. x1 is any real number.
For d = 2, g(x) = 2^x - x^2 >= 0,
if x >= x2. x2 is 4
For d = 3, g(x) = 2^x - x^3 >= 0,
if x >= x3. x3 is about 9.94
For d = 4, g(x) = 2^x - x^4 >= 0,
if x >= x4. x4 is 16
Because x is also called lambda, that is what means "lambda >= lambda d".
-Count

What does mean "lambda >= lambda d"?
Because the epsilon is a function, we can write the lambda as x and the epsilon as f(x) for easy understanding. We specify f(x) as below, that is an example,
f(x) = 1 / (2^x)
The f(x) is negligible because,
f(x) = 1 / (2^x) <= 1 / (x^d),
for all d and large enough x. (statement 1)
Why do we consider the statement 1 is true? I am not a mathematician. I prefer to use enough examples and tools to observe and understand problem. The tool, the iPad App Quick Graph+, is used to draw curves of the below functions.
f(x) = 1 / (2^x)
f(x) = 1 / x
f(x) = 1 / (x^2)
f(x) = 1 / (x^3)
f(x) = 1 / (x^4)

It is hard to verify the statement 1 with the picture because the curves are close to each other when x is large. Therefore we transfer the statement 1 as below.
g(x) = 2^x - x^d >= 0,
for all d and an enough large x. (statement 2)
We give examples, d = 1, 2, 3, 4. The below picture contains the curves.

If we zoom in the picture, we can find an interesting thing.
The statement 2 is true for an enough large x.

For d = 1, g(x) = 2^x - x >= 0,
if x >= x1. x1 is any real number.
For d = 2, g(x) = 2^x - x^2 >= 0,
if x >= x2. x2 is 4
For d = 3, g(x) = 2^x - x^3 >= 0,
if x >= x3. x3 is about 9.94
For d = 4, g(x) = 2^x - x^4 >= 0,
if x >= x4. x4 is 16
Because x is also called lambda, that is what means "lambda >= lambda d".
-Count
Tuesday, September 13, 2016
XOR encryption is a randomized algorithm
We exactly describe that One Time Pad (OTP) encryption, that uses XOR operation, is a randomized algorithm.
Below is the definition of Randomized Algorithms:
Below is the definition of Randomized Algorithms:
A cipher (E, D) over (K, M, C) is OTP, so that
c = E (k, m) = k xor m
K = M = C = {0, 1}^n
For the definition of Randomized Algorithms, if k and c are uniform random variables, the OTP encryption, E, is a randomized algorithm.
The k, selected in K, must be a uniform random variable for the reason,
Why is the c, calculated by the OTP encryption, also a uniform random variables? The question is same to proof the below formula that is the definition of uniform random variable.
Pr [c = c0] = 1 / |C|
Please remember that a random variable is really a function. So transform the formula to display the function E (k, m0),
Pr [c = c0] =
Pr [E (k, m0) = c0] =
OTP encryption uses XOR operation.
Pr [k xor m0 = c0] =
Pr [k = c0 xor m0] =
Pr [k = k0] = 1 / |K|
because there is only one k0 that encrypts m0 to generate c0.
Pr [c = c0] = 1 / |K| = 1 / |C|
because |K| = |C| = 2^n
We proof that the OTP encryption is a randomized algorithm.
-Count
My Proof for Shannon Theorem
In this topic, I use my informal way to proof Shannon Theorem. Yes, it is informal but easy to understand the theorem. I also proof that the substitute cipher is not perfect secrecy.
Shannon Theorem:
A cipher (E, D) over (K, M, C) has perfect secrecy
=>
|K| >= |M|
The theorem is identical the below statement.
|K| <= |M|
=>
A cipher doesn't have perfect secrecy
My proof of the theorem is to give an example.
Lets
K = {0, 1}, M = C = {0, 1}^2
We define the encryption algorithm E as below.
if k = 0,
m c
-----
00 00
01 01
10 10
11 11
if k = 1,
m c
-----
00 01
01 10
10 11
11 10
We use the below formula to verify if the cipher is perfect secrecy. It it is perfect secrecy,
Pr [E (k, m) = c] = constant
I use the both pairs
(m, c) = (00, 00) or (00, 10)
to verify it.
Pr [E (k, 00) = 00] = (# of keys) / |K| = 1/2,
Only one key, k=0, exists.
Pr [E (k, 00) = 10] = (# of keys) / |K| = 0/2 = 0,
We cannot find a key to make the equation.
Pr [E (k, m) = c] = 1/2 or 0
Obviously, it is not constant. Therefore the cipher is not perfect secrecy. We proof it. Actually, the cipher is called substitute cipher.
-Count
Shannon Theorem:
A cipher (E, D) over (K, M, C) has perfect secrecy
=>
|K| >= |M|
The theorem is identical the below statement.
|K| <= |M|
=>
A cipher doesn't have perfect secrecy
My proof of the theorem is to give an example.
Lets
K = {0, 1}, M = C = {0, 1}^2
We define the encryption algorithm E as below.
if k = 0,
m c
-----
00 00
01 01
10 10
11 11
if k = 1,
m c
-----
00 01
01 10
10 11
11 10
We use the below formula to verify if the cipher is perfect secrecy. It it is perfect secrecy,
Pr [E (k, m) = c] = constant
I use the both pairs
(m, c) = (00, 00) or (00, 10)
to verify it.
Pr [E (k, 00) = 00] = (# of keys) / |K| = 1/2,
Only one key, k=0, exists.
Pr [E (k, 00) = 10] = (# of keys) / |K| = 0/2 = 0,
We cannot find a key to make the equation.
Pr [E (k, m) = c] = 1/2 or 0
Obviously, it is not constant. Therefore the cipher is not perfect secrecy. We proof it. Actually, the cipher is called substitute cipher.
Tuesday, September 6, 2016
Why must the key of the encryption be random?
When I learn the Stanford online course, Cryptography I, I ask my self the question: "Why must the key of the encryption be random?"
The encryption algorithm is written below.
C = E (M, K)
where
C is ciphertext,
M is plaintext message,
K is a key,
E is an encryption algorithm.
We use XOR algorithm as encryption algorithm.
C = M XOR K.
The purpose is to make C an uniform random variable even though M is not, and specify:
Pr [M=0] = m0
If K is not an uniform random variable, then
k0 <> k1
Below is the table of the equation, C = M XOR K.
We can calculate that:
Pr [C=0] = m0 * k0 + m1 * k1 <> 1/2
Pr [C=1] = m0 * k1 + m1 * k0 <> 1/2
Thus C is not a uniform random variable.
I draw the below picture to explain why the two inequalities are right.
m0 * k0 + m1 * k1 <> 1/2
m0 * k1 + m1 * k0 <> 1/2

When I see the two areas m0 * k0 and m1 * k1, I FEEL that m0 * k0 + m1 * k1 <> 1/2.
In conclusion, if we want to build a ciphertext randomly, the key must be random.
We also make sure that XOR encryption is a randomized algorithm because if the key is a uniform random variable, the output ciphertext is also a uniform random variable.
The next page explain why XOR encryption is a randomized algorithm.
-Count
The encryption algorithm is written below.
C = E (M, K)
where
C is ciphertext,
M is plaintext message,
K is a key,
E is an encryption algorithm.
We use XOR algorithm as encryption algorithm.
C = M XOR K.
The purpose is to make C an uniform random variable even though M is not, and specify:
Pr [M=0] = m0
Pr [M=1] = m1
m0 + m1 = 1 and
m1 <> m2
m0 + m1 = 1 and
m1 <> m2
Pr [K=0] = k0
Pr [K=1] = k1
k0 + k1 = 1If K is not an uniform random variable, then
k0 <> k1
Below is the table of the equation, C = M XOR K.
| M | K | C | Probability |
| 0 | 0 | 0 | m0 * k0 |
| 0 | 1 | 1 | m0 * k1 |
| 1 | 0 | 1 | m1 * k0 |
| 1 | 1 | 0 | m1 * k1 |
We can calculate that:
Pr [C=0] = m0 * k0 + m1 * k1 <> 1/2
Pr [C=1] = m0 * k1 + m1 * k0 <> 1/2
Thus C is not a uniform random variable.
I draw the below picture to explain why the two inequalities are right.
m0 * k0 + m1 * k1 <> 1/2
m0 * k1 + m1 * k0 <> 1/2

When I see the two areas m0 * k0 and m1 * k1, I FEEL that m0 * k0 + m1 * k1 <> 1/2.
In conclusion, if we want to build a ciphertext randomly, the key must be random.
We also make sure that XOR encryption is a randomized algorithm because if the key is a uniform random variable, the output ciphertext is also a uniform random variable.
The next page explain why XOR encryption is a randomized algorithm.
-Count
Subscribe to:
Comments (Atom)












