How does a software engineer understand "Perfect Secrecy"?

I consider, a definition in mathematic formula format is like source code written with a computer language. Mathematic formula is written for mathematician. Source code is written for a computer.

The way to understand a mathematic definition is the same as the way to understand a source code. How do we understand source code? I believe any experienced software engineers know the trick. I also believe we can understand some mathematic definition in the same way for understanding source code.

Don't worry, we have enough ability to understand some mathematic definition. For example, below is the definition of "perfect secrecy":



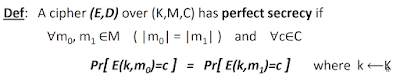
The definition is a formula that is compressed from many sentences. How do we understand it? A better way is try to decompress the formula to get original sentences and understand them.

We know that,

E(k, m) = c
D(k, c) = m

I explain the perfect secrecy that:

1. I know the ciphertext, c.
2. I know the encryption and decryption algorithms, E and D.
3. It is hard to guess the key, k, because it is a uniform random variable. The probability of successfully guessing is 1/|K|.
4. It is hard to get a correct m by decrypting c with a guessed key because the probability of getting the correct m is the same constant for all k in K.

Our purpose is to translate the four sentences into a formal definition with a formula.

First, try to translate the above sentences in a informal formula.

E(k?, m?) = c

It means:

• I know the ciphertext, c, and encryption algorithm, E.
• I don't know k and m.

Translate it into another informal formula.

E(k, m?) = c
where k is a uniform random variable on K

Because m is deterministic by D(k, c) = m, we translate it again.

E(k, mi) = c
where k is a uniform random variable on K

and i = 0, 1, ..., |M|

Finally we add the 4th sentence to complete the formal definition of "perfect secrecy".

Pr[E(k, mi) = c] = constant

where k is a uniform random variable on K

and i = 0, 1, ..., |M|

-Count